Generalization
기존의 전통적인 프로그래밍에서는 사람이 모든 경우의 수를 고려하여 명확한 조건과 규칙을 기반으로 결과를 도출했다. 이는 규칙을 기반으로 하기에 Rule-based System이라고도 한다. 하지만 우리가 다루는 데이터가 더욱 복잡해짐에 따라, 모든 경우의 수를 반영해서 프로그래밍 하는 것은 현실적으로 불가능해졌다.
이를 해결하기 위해 수집한 데이터에 있는 특성과 패턴을 파악해서 수집한 데이터 뿐만 아니라 보지 못한 모든 데이터에서도 잘 동작하는 능력인 일반화 능력을 가진 인공지능 모델을 개발하려 하는 것이다.

Underfitting and Overfitting
Underfitting은 모델의 일반화 성능을 따질 것도 없이 훈련 데이터 셋에 대해서도 잘 동작하지 않는 상태이다. 말그대로 모델이 데이터에 아직 덜 fitting되었다, 즉 덜 학습했다는 뜻이다.
Overfitting은 모델이 훈련 데이터 셋에 너무 딱 맞게 학습된 상태이다. 예를 들어 둥근 잎만 가진 나무를 학습했더라도 뾰족한 잎을 가진 나무도 나무라고 유연하게 판단할 수 있는 일반화 능력이 있어야 하는데, 너무 과도하게 세밀한 부분까지 학습해서 뾰족한 잎을 가진 나무를 나무라고 판단하지 않는 상태인 것이다.
모델 학습 전략
1. Make the training error small
먼저 Overfitting이 일어날 때까지 학습을 시켜본다. 입력과 정답이 모두 있는 Supervised Learning에서 모델을 충분히 학습했는데도 Underfitting 상태라면 데이터 문제든 모델 문제든 학습과정에 문제가 있는 것이다. 또한 처음 모델을 학습시킬 때 Overfitting을 통해 모델이 학습 데이터에 대한 Error를 어디까지 낮출 수 있는가를 아는 것은 중요하다.
Training Error를 낮출 수 있는 가장 간단한(?) 방법은 모델의 Capacity를 키우는 것이다. 모델의 Capacity가 커질수록 더 작은 특징까지 잡아낼 수 있기 때문에 Capacity가 커지면 커질수록 Training Error는 무조건 낮아진다.
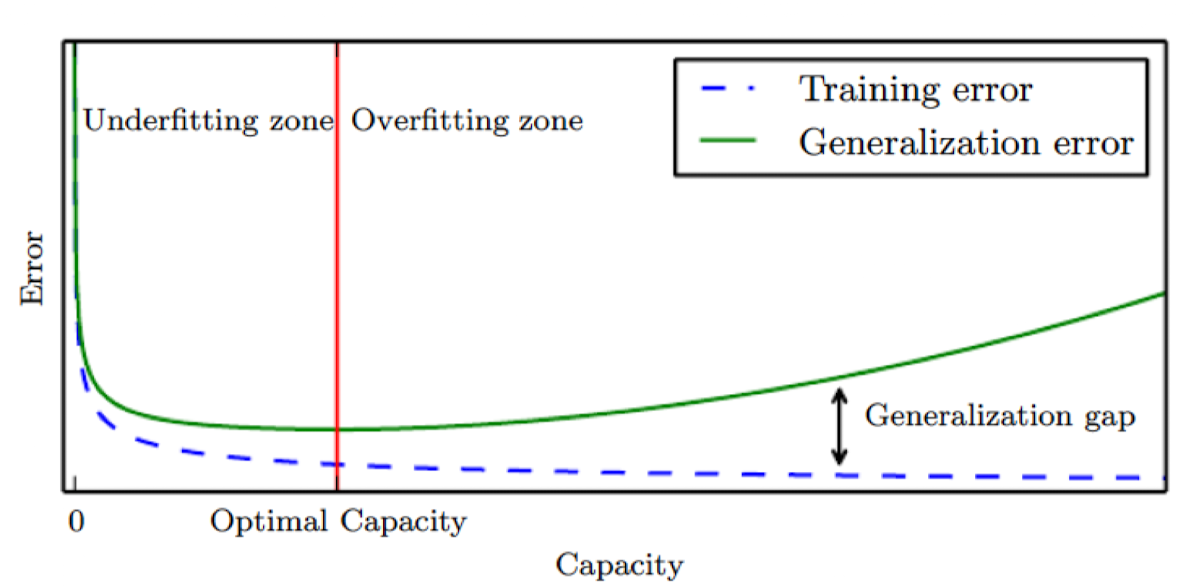
2. Make the gap between the training and test error small
하지만 우리는 Training Error를 낮추는 게 목적이 아니라 수집한 데이터와 수집하지 못한 데이터를 합친 Universal data에 대한 Generalization Error를 줄이는 게 목적이다. 이를 줄이기 위해서 가장 좋은 방법은 Training Data가 많은 것이다. (만약 모델의 Capacity가 낮아 아무리 학습시켜도 Underfitting이라면 Training Data가 많아도 모델이 데이터 표현 능력이 없으므로 소용이 없다.)
하지만 현실적으로 Data를 늘리는 것은 한계가 있으므로 Regularization과 같은 기법을 통해 Training Error가 조금 높아지더라도 Test Error를 낮춘다. (Regularization은 Loss에 Training Error 뿐만 아니라 모델의 Capacity를 최소화하는 항을 추가해 학습하는 기법이다.)
Bias-Variance Trade Off
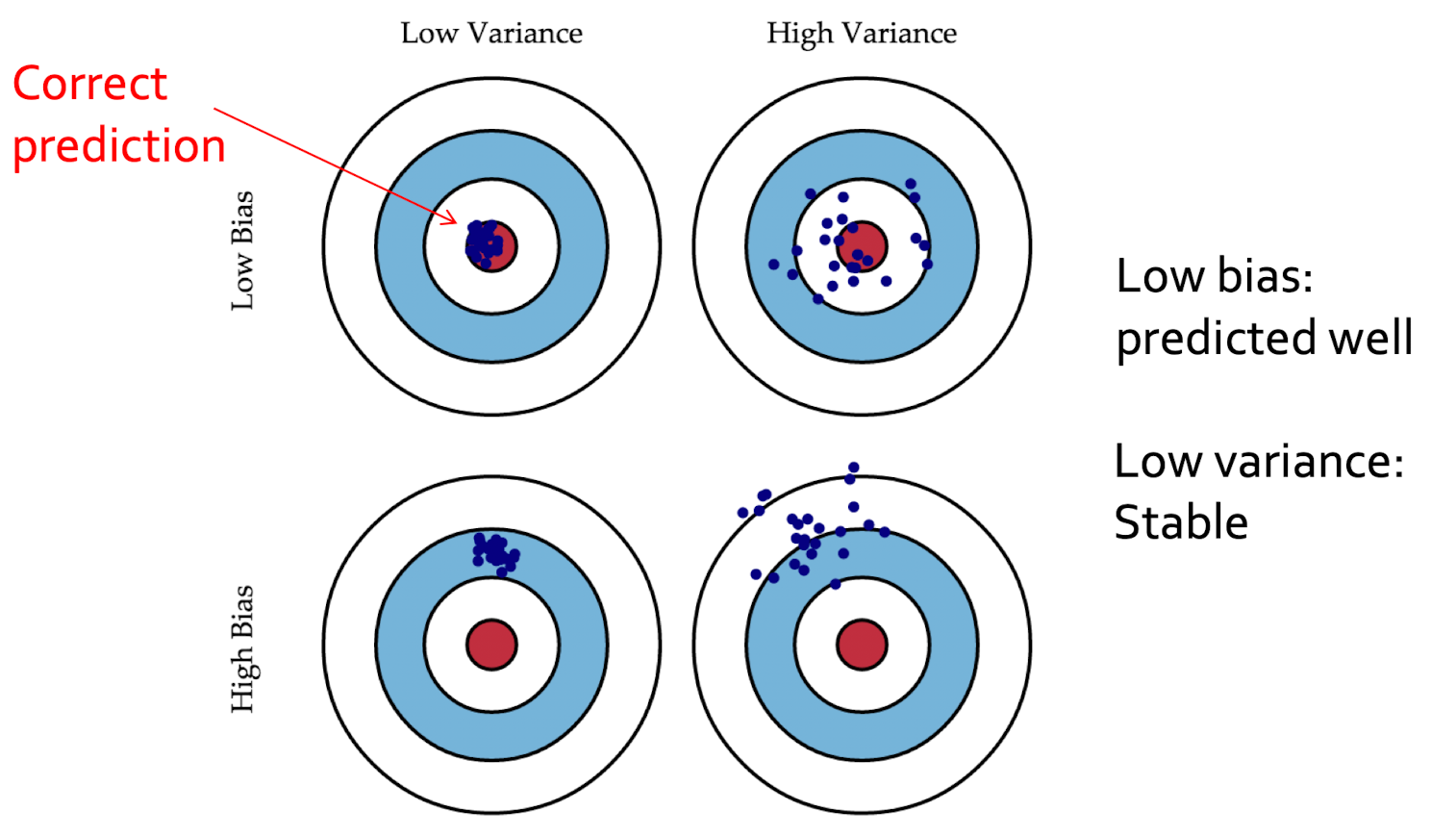
모델의 Test Error를 줄이기 위해서는 모델의 Bias와 Variance를 둘 다 낮춰야 한다고 한다. 그런데 Bias를 낮추면 Variance가 올라가고, Variance를 낮추면 Bias가 올라가는 데, 이러한 둘의 관계를 Bias-Variance Trade Off라고 한다.
그러면 Bias와 Variance는 무엇을 뜻하는 걸까?
이를 설명할 때 가장 많이 사용하는 과녁 그림을 보면 중앙으로 예측하는 것이 목표이고 실제 모델의 예측은 파란 점이다. Bias란 파란 점의 평균이 중앙과 얼마나 차이나는지를 뜻하고, Variance란 각각의 예측들이 모델의 평균과 얼마나 차이나는지, 즉 얼마나 분산되어 있는지를 나타낸다. 하지만 이는 Bias와 Variance의 정의를 말할 뿐 이것이 모델의 일반화 성능을 표현하는데 어떤 관계가 있는지 잘 와닿지 않는다.
나는 처음에 Bias가 편향이라는 뜻이니까 학습데이터에 너무 편향되게 학습되었다는 뜻이라고 잘못 이해했고, 만약 그렇다면 Test에 대해서 예측이 이리저리 튀는 Variance도 같이 커져야 하는게 아닌가라는 궁금점을 가졌었다.
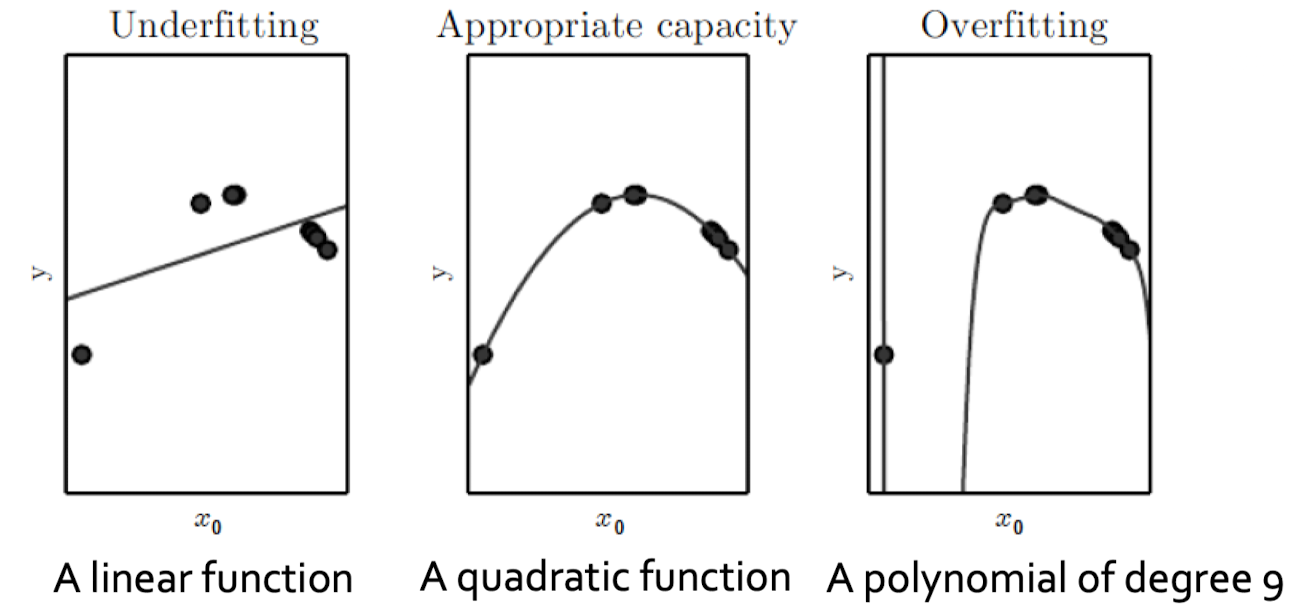
하지만 Bias는 학습 데이터에 과도하게 편향된 것을 뜻하는게 아니라, 모델이 데이터를 너무 단순하게 해석해서 편향된 것을 뜻한다. High Bias, Low Variance란 모델이 데이터를 너무 단순하게 해석하기 때문에 학습하지 못한 데이터가 들어와도 예측값이 튀지는 않지만 학습한 부분조차 잘 예측하지 못하는 것이다. 아래 그림에서 Linear function을 뜻한다.
반대로 Low Bias, High Variance는 모델이 데이터의 작은 변화에도 민감하게 반응할 수 있는 능력이 있어서 학습 데이터에 더 fit하게 학습되지만, 학습하지 못한 부분에 대해서는 예측값이 이리저리 튄다. 아래 그림에서 Polynomial of degree 9을 뜻한다. Polynomial of degree 9의 왼쪽 부분은 학습하지 못한 부분이라 그래프가 튀는 것을 볼 수 있다.
과녁 그림의 직관적 이해

내가 생각했을 때 과녁 사진을 모델 학습에 정확히 비유하려면, 이 과녁이 창던지기 과녁이라고 생각하면 좋을 듯하다.
High Bias, Low Variance의 상황은 선수가 안 써본 창을 써도 일관되게 던질 수 있는 능력은 있지만, 애초에 과녁 중앙까지 던질 수 있는 힘이 없는 것이라 생각할 수 있다. (모델 측면에서는 학습 하지 않은 데이터에 대해 일관적이게 예측하지만, 애초에 학습한 데이터도 정답과 오차가 있는 것.)
Low Bias, High Variance의 상황은 선수가 과녁 중앙까지 던질 수 있는 힘은 충분하지만, 연습해 본 창만 잘 던지는 선수라서 안 써본 창을 쓰면 일관되게 던질 수가 없는 것이다. (모델 측면에서는 학습한 데이터는 잘 예측하지만, 학습 하지 않은 데이터에 대해서는 일관적이지 않게 예측하는 것.)
'Deep Learning' 카테고리의 다른 글
| GPT-3, InstructGPT, GPT-4 정리 (0) | 2025.02.02 |
|---|---|
| 정보이론 기초 (0) | 2023.02.09 |
Generalization
기존의 전통적인 프로그래밍에서는 사람이 모든 경우의 수를 고려하여 명확한 조건과 규칙을 기반으로 결과를 도출했다. 이는 규칙을 기반으로 하기에 Rule-based System이라고도 한다. 하지만 우리가 다루는 데이터가 더욱 복잡해짐에 따라, 모든 경우의 수를 반영해서 프로그래밍 하는 것은 현실적으로 불가능해졌다.
이를 해결하기 위해 수집한 데이터에 있는 특성과 패턴을 파악해서 수집한 데이터 뿐만 아니라 보지 못한 모든 데이터에서도 잘 동작하는 능력인 일반화 능력을 가진 인공지능 모델을 개발하려 하는 것이다.

Underfitting and Overfitting
Underfitting은 모델의 일반화 성능을 따질 것도 없이 훈련 데이터 셋에 대해서도 잘 동작하지 않는 상태이다. 말그대로 모델이 데이터에 아직 덜 fitting되었다, 즉 덜 학습했다는 뜻이다.
Overfitting은 모델이 훈련 데이터 셋에 너무 딱 맞게 학습된 상태이다. 예를 들어 둥근 잎만 가진 나무를 학습했더라도 뾰족한 잎을 가진 나무도 나무라고 유연하게 판단할 수 있는 일반화 능력이 있어야 하는데, 너무 과도하게 세밀한 부분까지 학습해서 뾰족한 잎을 가진 나무를 나무라고 판단하지 않는 상태인 것이다.
모델 학습 전략
1. Make the training error small
먼저 Overfitting이 일어날 때까지 학습을 시켜본다. 입력과 정답이 모두 있는 Supervised Learning에서 모델을 충분히 학습했는데도 Underfitting 상태라면 데이터 문제든 모델 문제든 학습과정에 문제가 있는 것이다. 또한 처음 모델을 학습시킬 때 Overfitting을 통해 모델이 학습 데이터에 대한 Error를 어디까지 낮출 수 있는가를 아는 것은 중요하다.
Training Error를 낮출 수 있는 가장 간단한(?) 방법은 모델의 Capacity를 키우는 것이다. 모델의 Capacity가 커질수록 더 작은 특징까지 잡아낼 수 있기 때문에 Capacity가 커지면 커질수록 Training Error는 무조건 낮아진다.

2. Make the gap between the training and test error small
하지만 우리는 Training Error를 낮추는 게 목적이 아니라 수집한 데이터와 수집하지 못한 데이터를 합친 Universal data에 대한 Generalization Error를 줄이는 게 목적이다. 이를 줄이기 위해서 가장 좋은 방법은 Training Data가 많은 것이다. (만약 모델의 Capacity가 낮아 아무리 학습시켜도 Underfitting이라면 Training Data가 많아도 모델이 데이터 표현 능력이 없으므로 소용이 없다.)
하지만 현실적으로 Data를 늘리는 것은 한계가 있으므로 Regularization과 같은 기법을 통해 Training Error가 조금 높아지더라도 Test Error를 낮춘다. (Regularization은 Loss에 Training Error 뿐만 아니라 모델의 Capacity를 최소화하는 항을 추가해 학습하는 기법이다.)
Bias-Variance Trade Off

모델의 Test Error를 줄이기 위해서는 모델의 Bias와 Variance를 둘 다 낮춰야 한다고 한다. 그런데 Bias를 낮추면 Variance가 올라가고, Variance를 낮추면 Bias가 올라가는 데, 이러한 둘의 관계를 Bias-Variance Trade Off라고 한다.
그러면 Bias와 Variance는 무엇을 뜻하는 걸까?
이를 설명할 때 가장 많이 사용하는 과녁 그림을 보면 중앙으로 예측하는 것이 목표이고 실제 모델의 예측은 파란 점이다. Bias란 파란 점의 평균이 중앙과 얼마나 차이나는지를 뜻하고, Variance란 각각의 예측들이 모델의 평균과 얼마나 차이나는지, 즉 얼마나 분산되어 있는지를 나타낸다. 하지만 이는 Bias와 Variance의 정의를 말할 뿐 이것이 모델의 일반화 성능을 표현하는데 어떤 관계가 있는지 잘 와닿지 않는다.
나는 처음에 Bias가 편향이라는 뜻이니까 학습데이터에 너무 편향되게 학습되었다는 뜻이라고 잘못 이해했고, 만약 그렇다면 Test에 대해서 예측이 이리저리 튀는 Variance도 같이 커져야 하는게 아닌가라는 궁금점을 가졌었다.
하지만 Bias는 학습 데이터에 과도하게 편향된 것을 뜻하는게 아니라, 모델이 데이터를 너무 단순하게 해석해서 편향된 것을 뜻한다. High Bias, Low Variance란 모델이 데이터를 너무 단순하게 해석하기 때문에 학습하지 못한 데이터가 들어와도 예측값이 튀지는 않지만 학습한 부분조차 잘 예측하지 못하는 것이다. 아래 그림에서 Linear function을 뜻한다.
반대로 Low Bias, High Variance는 모델이 데이터의 작은 변화에도 민감하게 반응할 수 있는 능력이 있어서 학습 데이터에 더 fit하게 학습되지만, 학습하지 못한 부분에 대해서는 예측값이 이리저리 튄다. 아래 그림에서 Polynomial of degree 9을 뜻한다. Polynomial of degree 9의 왼쪽 부분은 학습하지 못한 부분이라 그래프가 튀는 것을 볼 수 있다.

과녁 그림의 직관적 이해

내가 생각했을 때 과녁 사진을 모델 학습에 정확히 비유하려면, 이 과녁이 창던지기 과녁이라고 생각하면 좋을 듯하다.
High Bias, Low Variance의 상황은 선수가 안 써본 창을 써도 일관되게 던질 수 있는 능력은 있지만, 애초에 과녁 중앙까지 던질 수 있는 힘이 없는 것이라 생각할 수 있다. (모델 측면에서는 학습 하지 않은 데이터에 대해 일관적이게 예측하지만, 애초에 학습한 데이터도 정답과 오차가 있는 것.)
Low Bias, High Variance의 상황은 선수가 과녁 중앙까지 던질 수 있는 힘은 충분하지만, 연습해 본 창만 잘 던지는 선수라서 안 써본 창을 쓰면 일관되게 던질 수가 없는 것이다. (모델 측면에서는 학습한 데이터는 잘 예측하지만, 학습 하지 않은 데이터에 대해서는 일관적이지 않게 예측하는 것.)
'Deep Learning' 카테고리의 다른 글
| GPT-3, InstructGPT, GPT-4 정리 (0) | 2025.02.02 |
|---|---|
| 정보이론 기초 (0) | 2023.02.09 |
