정보이론 기초

정보이론이란?

정보이론이란 정보의 가치를 어떻게 나타낼 지에 대한 아이디어라고 할 수 있다.

 

예를 들어 '집값이 10억 오를 예정이다'라는 정보는 굉장히 가치가 크지만, '영화가 재밌다'라는 정보는 가치가 적다고 할 수 있다.

 

이런 정보이론은 대표적으로 통신, 압축에 많이 사용된다.

 

우리가 사용하는 핸드폰 요금제를 보면 10GB 요금제처럼 비트를 기준으로 책정한 요금제들이 있다.

즉, 요금을 핸드폰에 오고 간 비트의 양만큼 책정하는 것이다.

이때 이 비트를 효율적으로 통신하고자 사용하는 것이 정보이론이다.

 

우리는 항상 모든 정보를 똑같은 비율로 사용하지 않는다.

예를 들어 카톡에서 'ㅋ'는 많이 사용하지만, '윿'과 같은 이상한 문자는 거의 사용하지 않는다.

고로 'ㅋ'는 적은 비트수를 할당하고 '윿'은 많은 비트수를 할당해서 통신을 하면 균일하게 할당할 때보다 비트 사용량을 줄일 수 있다.

 

예를 들어 'ㅋㅋㅋㅋ윿'을 보낸다고 생각해보자.

비트를 2개로 균일하게 할당한다고 생각하면 총 10비트가 사용되는데, 'ㅋ'는 1개로 '윿'은 3개로 할당하면 총 7비트가 사용된다.

두 단어의 평균 비트수는 동일하지만 사용된 총 비트수는 훨씬 적은 것이다.

 

이와 같이 정보이론에서 다루는 것들은 정보를 비트로 표현하자는 아이디어 아래에서 확장되는 개념들이라고 볼 수 있고, 이는 압축에도 동일하게 적용된다.

 

Entropy

물리에서의 엔트로피는 '무질서도'라고 배운다.

하지만 정보이론에서의 엔트로피는 '정보를 표현하는데 필요한 최소 평균 비트수'이다.

 

카톡 예시에서 정보들은 각자의 발생 확률을 지니고 있고 확률이 높은 정보는 낮은 비트수를, 확률이 낮은 정보는 높은 비트수를 사용하는게 효율적임을 봤다.

즉, 엔트로피는 확률에 의거해 가장 효율적으로 비트가 사용되었을 때의 총 비트수를 정보의 개수로 나눈 최소 평균 비트수인 것이다. (그 어떤 경우에도 이보다 더 효율적으로 비트를 사용할 수 없다.)

 

확률이 높은 정보는 낮은 비트수를 사용하므로 이를 아래 $-\log_2(x)$로 사용할 수 있다.

(비트로 표현을 하는 것이므로 로그의 밑은 2이다.)

 

확률이 높을수록 비트수는 작아진다.

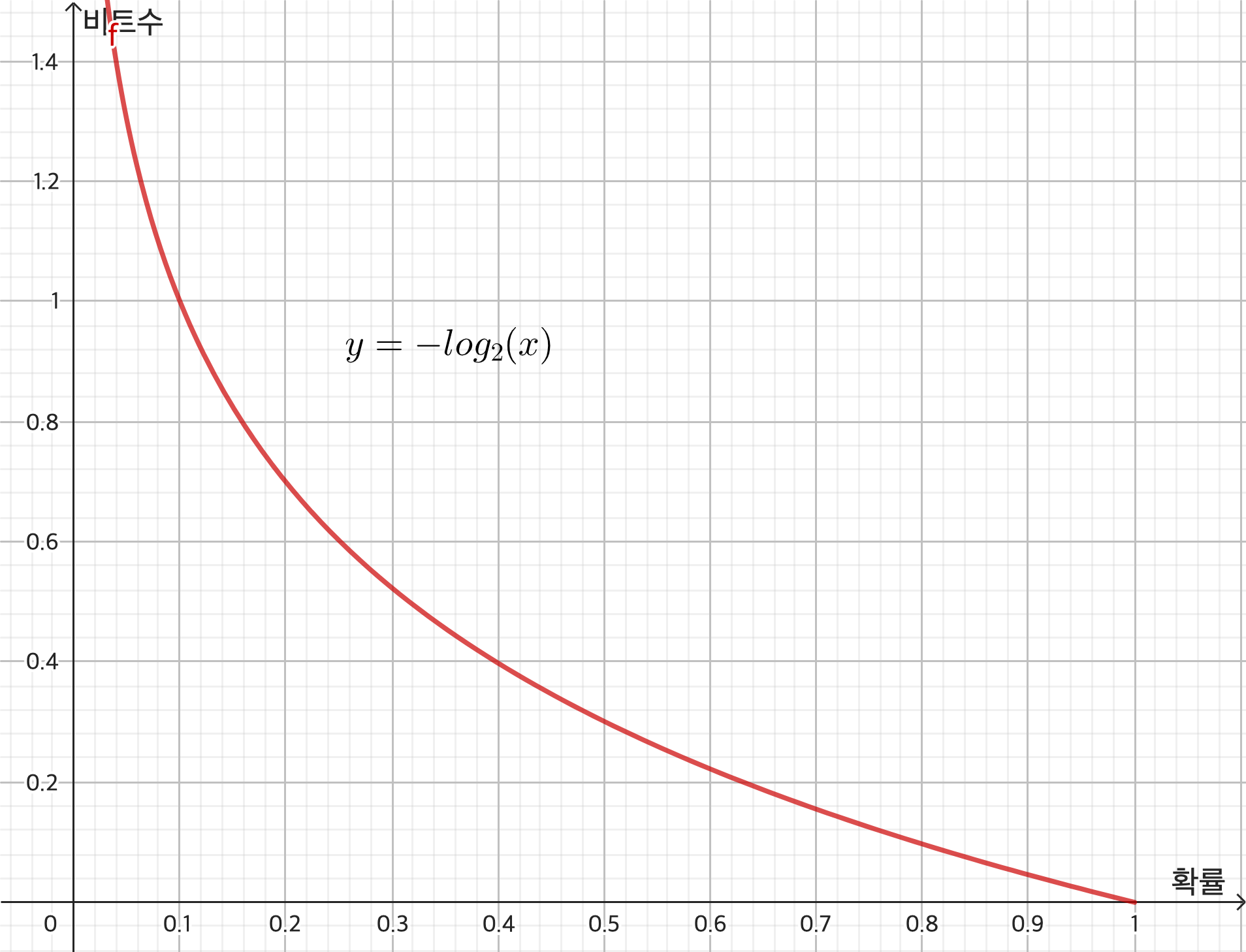
x는 확률이므로 0부터 1사이의 값을 가짐을 알 수 있다. (y축은 정확히 비트수가 아니라 비트수를 나타내는 어떤 계수라고 할 수 있다.)

 

또, 확률이므로 그냥 평균이 아닌 기대값을 계산해야 한다.

고로 $ E_n = \sum_i -p_i \log_2 p_i$이다.

 

그리고 엔트로피는 이 확률들의 분포가 균등분포일 때 최대가 된다.

(연속적인 경우는 $ E_n = -\int P(x) \ln{P(x)}dx$이고, 확률분포가 가우시안 분포일 때 최대가 된다.)

 

Cross-Entropy & KL-divergence

CrossEntropy는 Entropy에서의 이상적인 확률분포가 아닌 측정했을 때의 확률분포의 엔트로피이다.

 

Entropy에서의 확률은 이상적인 확률분포를 따르는 $p_i$이지만

CrossEntropy는 측정한 확률 분포를 따르는 $q_i$를 사용해서 $ CE_n = \sum_i -p_i \log_2 q_i$로 나타낼 수 있다.

 

그리고 엔트로피는 가장 최소가 되는 비트수를 나타내므로 항상 Cross-Entropy는 항상 Entropy보다 클 수 밖에 없다.

 

그렇다면 이 CrossEntropy는 항상 Entropy에 비해 비효율적이라 할 수 있는데 이 비효율적인 정도를 나타내는 것을 KL-divergence라고 한다.

이 KL-divergence는 단순히 CrossEntropy에서 Entropy을 뺀 것으로 $KL = -\sum_i p_i \log_2 q_i + \sum_i p_i \log_2 p_i$

 

즉, $\sum_i p_i \log{\cfrac{p_i}{q_i}}$이다.

(참고로 딥러닝에서 최적화하고 싶은 것은 $q$이므로 비용함수로 CE를 하나, KL을 하나 똑같은 결과를 가져온다고 할 수 있다.)

 

Mutual information

Mutual information의 정의는 $\sum_i\sum_j P(x_i, y_i) \log {\cfrac{P(x_i, y_i)}{P(x_i)P(y_i)}}$이다.

 

KL-divergence의 식을 보면 $KL = \sum_i p_i \log{\cfrac{p_i}{q_i}}$로 Mutual information과 흡사한 구조인 것을 볼 수 있다.

 

KL-divergence의 뜻을 다시 살펴보면 이상적으로는 $p_i$이지만 실제로 측정했더니 $q_i$일 때 얼마나 비효율적인가를 나타낸 것이다.

그렇다면 Mutual information 또한, 이상적으로는 $P(x_i, y_i)$이지만 실제로 측정해서 $P(x_i)P(y_i)$일 때 얼마나 비효율적인가를 나타낸 것이라고 볼 수 있다.

 

그런데 우리는 $P(x_i, y_i)$가 독립이면 $P(x_i)P(y_i)$임을 알고 있다.

그렇다면 Mutual information은 이상적으로는 $x_i, y_i$가 독립이 아닌데, 독립이라고 생각했을 때 얼마나 비효율적인가, 얼마나 차이가 나는가를 나타낸 것임을 알 수 있다.

 

또한 이를 토대로 Mutual information은 독립이 아닌 정도가 심하면 심할수록 값이 커진다는 것을 짐작할 수 있다.

반대로 독립이라면 0이 된다.